The Monty Hall Problem, Proven with Python (and Math)

image source: https://paulvanderlaken.com/2020/04/14/simulating-visualizing-monty-hall-problem-python-r/

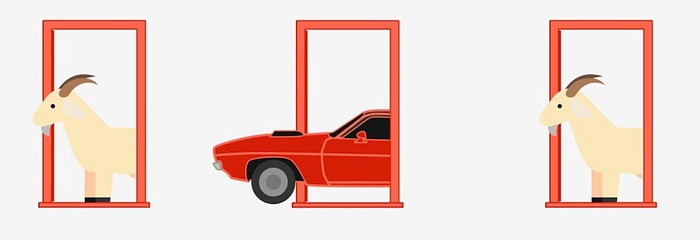
When the movie 21 came out in 2008, I remember one scene that never quite sat right with me. MIT statistics professor Micky Rosa (played, unfortunately, by Kevin Spacey) offers an extra credit problem to his lecture hall. He demonstrates what in probability theory is known as the Monty Hall problem, named after the Let’s Make a Deal game show host. Professor Rosa tells Ben Campbell (played by Jim Sturgess) that Ben is a contestant on a game show. There are 3 doors. Hidden behind one of them is a new car. The other two? Goats. Ben picks door #1.

This is where things get interesting. The game show host (who knows what’s behind each door) decides to reveal that door #3 is hiding a goat. Ben has a second chance to choose a door. He can either stick with his first choice, door #1, or switch to door #2. Ben chooses to switch. When asked “so how do you know [the host] isn’t trying to play a trick on you? Trying to use reverse psychology to get you to pick a goat?”, Ben explains that it doesn’t matter. His answer is based on statistics, variable change, specifically. When he initially picked a door, he had a 33.3% chance of picking the car. Now that the host has taken away the last door, he’s got a 66.7% if he chooses to switch.

For years, this seemed like the least intuitive answer to me. Each door has an equal chance of having a car. What does it matter what the last door had? It should be 50/50 now. I’m the kind of person who needs to see something proven myself before I can fully commit to believing it. So that’s what I set out to do. The math goes roughly like this:

Q.E.D.
But I still wasn’t totally happy with this explanation. I wanted to see it in action. So, for you more computer-science oriented folks, the following Python code should be easy to follow and reproduce on your own machine.

import numpy as np
np.random.seed(21)
doors = ['1', '2', '3']
second_choices = ['stay', 'switch']
# simulation function
def simulation(first_choice='1', second_choice='stay', n_trials=10_000):
    win_count = 0
    
    for i in range(n_trials):
        # putting car behind door A, B, or C at random (w/ equal prob for each)
        car_location = np.random.choice(doors)
        
        # host must show door with a goat that we haven't chosen already
        door_shown = np.random.choice([door for door in doors if door not in (first_choice, car_location)])
if second_choice == 'stay':
            final_door = first_choice
        else: # switch
            final_door = np.random.choice([door for door in doors if door not in (first_choice, door_shown)])
    
        if final_door == car_location:
            win_count += 1
win_ratio = win_count / n_trials
    
    print(f'Win ratio for initially choosing door #{first_choice} then {second_choice}ing is {win_ratio}')
    return

To finally give me the output

Win ratio for initially choosing door #1 then staying is 0.329
Win ratio for initially choosing door #2 then staying is 0.3331
Win ratio for initially choosing door #3 then staying is 0.3369
Win ratio for initially choosing door #1 then switching is 0.6673
Win ratio for initially choosing door #2 then switching is 0.6653
Win ratio for initially choosing door #3 then switching is 0.6626

We can reasonably infer from the above results that the underlying probability of being correct when staying is 1/3 whereas the probability of being correct when switching is 2/3. The Central Limit Theorem comes into play here. We probably would have been fine to only run a a few dozen trials on each, as the average value of these samples will soon approach the mean, but our findings are further validated by the 10,000 simulations ran on each of the six game options.

In conclusion, as unintuitive as it may seem, we have proven through both mathematical reasoning and a Python simulation that the answer to the Monty Hall problem is to always switch doors. Q.E.D.